Pengumpulan Data dalam Astronomi

Objek yang dikaji dalam astronomi yaitu benda langit. Padahal, benda langit ada banyak. Di Tata Surya saja, ada sebuah bintang, delapan planet, ratusan satelit, ribuan asteroid, puluhan benda kecil, dan ribuan komet. Untuk menghindari kebingungan, disusun cara menyatakan posisi benda langit.

Umumnya, astronom mengamati benda langit dari permukaan Bumi. Dari permukaan Bumi, benda langit tampak bergerak pada bola langit. Inilah sebabnya rujukan kebanyakan sistem koordinat langit berupa besaran-besaran kebumian. Dalam pencatatan posisi benda langit, Bumi dianggap sebagai pusat langit. Selain itu, informasi jarak tidak disertakan.

It Works, Globally

Dalam Alamat Bintang, dijelaskan sistem koordinat horizon. Tinjaulah kasus pengamatan di khatulistiwa! Lintasan Matahari tegak lurus terhadap bidang cakrawala. Di utara khatulistiwa, lintasan Matahari condong ke selatan. Sementara itu di selatan khatulistiwa, lintasan Matahari condong ke utara. Dengan demikian, sistem koordinat horizon berlaku lokal, bukan global.

Pengamatan dapat dilakukan di mana saja. Jika data pengamatan disampaikan pada pengamat dari lokasi lain menggunakan sistem koordinat horizon, dapat terjadi kebingungan. Karena itu, dikembangkan sistem koordinat ekuatorial, yang berlaku global. Sistem koordinat ini pada dasarnya merupakan perluasan sistem koordinat geografi ke bola langit. Rujukan sistem ini yaitu ekuator langit dan titik Aries. Titik Aries yaitu posisi Matahari ketika tepat di ekuator langit dan Belahan Bumi Utara mengalami musim semi.

Gambar 1. Posisi-posisi Bumi saat ekuinoks dan titik balik Matahari. -- Klik pada gambar untuk memperbesar!

Dalam sistem koordinat geografi, posisi lokasi terhadap ekuator disebut lintang, sedangkan posisi lokasi terhadap Greenwich disebut bujur. Sementara itu dalam sistem koordinat langit, posisi benda langit terhadap ekuator langit disebut deklinasi, sedangkan posisi benda langit terhadap titik Aries disebut asensiorekta. Nilai deklinasi bervariasi dari -90° hingga 90°, dengan tanda negatif berarti di selatan ekuator. Nilai asensiorekta bervariasi dari 0h hingga 24h, diukur ke arah timur, dengan 1h sama dengan 15°.

Gambar 2. Koordinat ekuatorial merupakan perluasan koordinat geografi ke bola langit. Ekuator langit sebidang dengan ekuator Bumi. Ekliptika yaitu posisi tahunan Matahari terhadap bola langit. -- Klik pada gambar untuk memperbesar!

To Move, Or Not To Move

Benda langit sebenarnya memang bergerak, namun pergerakannya sangat kecil jika dilihat dari Bumi. Penampakan bergeraknya benda langit dari timur ke barat terutama disebabkan oleh rotasi Bumi. Selain itu, garis edar benda langit akan berbeda jika dilihat dari lintang yang berbeda.

Gambar 3. Orientasi pengamat pada lintang 0°, 30°LU, 60°LS, dan 90°LS terhadap ekuator. -- Klik pada gambar untuk memperbesar!

Jika ditinjau dari bidang pengamatan, yang bervariasi yaitu orientasi ekuator terhadap bidang pengamatan. Hal ini ditunjukkan pada gambar di bawah.

Gambar 4. Variasi orientasi ekuator terhadap bidang pengamatan pada lintang 0°, 30°LU, 60°LS, dan 90°LS. -- Klik pada gambar untuk memperbesar!

Jika orientasi ekuator terhadap bidang pengamatan diketahui, dapat diketahui pula garis edar benda langit dengan deklinasi tertentu. Pada gambar di bawah, ditunjukkan garis edar Matahari pada tanggal 21 Desember, yang deklinasinya -23,5°.

Gambar 5. Garis edar Matahari pada tanggal 21 Desember di lintang 0°, 30°LU, 60°LS, dan 90°LS. -- Klik pada gambar untuk memperbesar!

Lintasan benda langit sejajar dengan ekuator. Selain itu jika deklinasinya negatif, lintasan benda langit berada di selatan ekuator.

Look Into Infinity and Beyond

Tanpa alat bantu, planet tampak sebagai titik bercahaya di langit. Tidak banyak yang dapat diketahui tentang titik bercahaya ini selain tentang posisi dan pola geraknya.

Dengan teleskop, dapat diamati bentuk planet. Hal ini dimungkinkan oleh sifat pembiasan cahaya ketika melewati lensa. Dalam konteks teleskop, lensa yang banyak digunakan yaitu lensa cembung. Pada lensa cembung, 1) berkas sinar sejajar dikumpulkan di titik fokus dan 2) berkas sinar yang melewati pusat lensa diteruskan tanpa dibelokkan.

Gambar 6. Berkas sinar yang melalui lensa cembung untuk kasus terbentuknya bayangan nyata.

Jika f yaitu titik fokus, s posisi benda, dan s' posisi bayangan benda, berlaku hubungan berikut.

\\\frac{1}{s}+\frac{1}{s'}=\frac{1}{f}\cdots\cdots\left(1\right)

Perbesaran bayangan, M, dirumuskan sebagai berikut.

M=\frac{s'}{s}\\\Rightarrow M=\frac{f}{s-f}\cdots\cdots\left(2a\right)\\\Rightarrow M=\frac{s'-f}{f}\cdots\cdots\left(2b\right)

Bayangan nyata memiliki perbesaran positif, sedangkan bayangan maya memiliki perbesaran negatif.

Gambar 7. Berkas sinar yang melalui lensa cembung untuk kasus terbentuknya bayangan maya.

Bayangan maya lebih mudah dilihat daripada bayangan nyata. Ini karena bayangan maya selalu berada di depan lensa sehingga hampir selalu terlihat jika mata berada dekat dengan lensa. Sementara itu untuk melihat bayangan nyata, jarak mata dari lensa harus diatur sesuai dengan hubungan (1). Karena itu jika mata yang digunakan untuk melihat bayangan benda, sebaiknya bayangan akhir yang terjadi merupakan bayangan maya. Posisi benda langit sangat jauh dari pengamat sehingga berkas sinar yang datang dapat dianggap sejajar. Dari asumsi ini dan hubungan (1), berlaku hubungan berikut pada lensa objektif.

\\s'_{obj}=\lim_{s_{obj}\to\infty}\frac{f_{obj}\cdot s_{obj}}{s_{obj}-f_{obj}}=f_{obj}\cdots\cdots\left(3\right)

Gambar 8. Sistem optik dengan dua lensa, seperti yang ada pada teleskop sederhana.

Bayangan lensa objektif bersifat nyata dan berfungsi sebagai benda bagi lensa okuler. Karena jarak bayangan ini dari okuler sama dengan fokus lensa okuler, berlaku hubungan berikut.

\\s'_{oku}=\lim_{s_{oku}\to\infty}\frac{f_{oku}\cdot s_{oku}}{s_{oku}-f_{oku}}=\infty\cdots\cdots\left(4\right)

Berikut persamaan perbesaran teleskop.

M_{tele}=\lim_{s_{obj}\to\infty ,s'_{oku}\to\infty}M_{obj}\cdot M_{oku}\\\Rightarrow M_{tele}=\lim_{s_{obj}\to\infty ,s'_{oku}\to\infty}\frac{s'_{obj}}{s_{obj}}\cdot\frac{s'_{oku}}{s_{oku}}\\\Rightarrow M_{tele}=\frac{s'_{obj}}{s_{oku}}\\\Rightarrow M_{tele}=\frac{f_{obj}}{f_{oku}}\cdots\cdots\left(5\right)

Measuring the Light

Fotometri yaitu pengukuran kecerlangan bintang. Tanpa alat bantu sekalipun, dapat ditentukan mana bintang yang lebih terang dari yang lainnya. Masalahnya yaitu "terang" atau "redup" merupakan penilaian subjektif; dibutuhkan penilaian baku yang objektif.

Kecerlangan bintang dinyatakan dalam besaran magnitudo melalui hubungan berikut.

m_2-m_1=-2,5\log\left(\frac{I_2}{I_1}\right)\cdots\cdots\left(6\right)

Besaran m yaitu magnitudo dan I yaitu fluks radiasi bintang. Fluks radiasi yaitu energi dari bintang per detik per luas area pada jarak tertentu dari bintang. Satuan fluks radiasi yaitu J.m^-2.s^-1. Makin terang suatu bintang, makin kecil magnitudonya.

Gambar 9. Foto gugus Pleiades. Bintang yang lebih terang nampak lebih besar. (NASA/ESA/AURA/Caltech/Palomar Observatory)

Fluks radiasi diterima pada jarak tertentu dari bintang. Jadi makin jauh jarak dari bintang, makin kecil fluksnya. Dampaknya yaitu kecerlangan bintang tergantung pada 1) energi yang dihasilkan per detik dan 2) jaraknya dari pengamat. Berikut perluasan hubungan (6).

m_2-m_1=-2,5\log\left(\frac{I_2}{I_1}\right)\\\Rightarrow m_2-m_1=-2,5\log\left(\frac{L_2/4\pi D_2^2}{L_1/4\pi D_1^2}\right)\\\Rightarrow m_2-m_1=-2,5\log\left(\frac{L_2}{L_1}\frac{D_1^2}{D_2^2}\right)\cdots\cdots\left(7\right)

Besaran L yaitu luminositas bintang dan D jarak bintang dari pengamat. Luminositas yaitu energi yang dipancarkan bintang per detik ke segala arah. Satuan untuk luminositas yaitu J.s^-1.

Gambar 10. Contoh tampilan intensitas piksel foto bintang pada perangkat lunak Iris. Nilai intensitas piksel kedua bintang ditandai dengan kotak merah.

Dengan perangkat lunak pengolah citra, dapat dihitung nilai intensitas piksel foto bintang. Intensitas piksel jelas tidak sama dengan fluks radiasi, tetapi berbanding lurus dengan fluks radiasi. Dengan demikian jika diketahui perbandingan intensitas piksel dua bintang, dapat diketahui pula selisih magnitudo kedua bintang tersebut.

Spectrum of Stars

Spektroskopi yaitu penguraian cahaya bintang. Dari spektroskopi, dapat diketahui, di antaranya, jenis zat pada bintang.

Gambar 11. Spektrum langit, dengan garis-garis serapan unsur-unsur di atmosfer dan Matahari. (Eric Bajart/G. Maureen)

Setiap benda bertemperatur pasti memancarkan gelombang elektromagnetik. Jika temperaturnya rendah, kebanyakan sinarnya berupa inframerah. Jika temperaturnya sangat tinggi, kebanyakan sinarnya berupa ultraviolet. Jika sinar ini melalui prisma, akan terbentuk spektrum kontinu.

Gambar 12. Spektrum kontinu dari benda bertemperatur.

Gambar 13. Lava dengan temperatur 1.000-1.200°C. Lava memancarkan sinar pada semua panjang gelombang, namun yang paling tinggi intensitasnya yaitu sinar merah-kuning. (Hawaii Volcano Observatory)

Radiasi dengan frekuensi tertentu yang diterima gas bertekanan rendah digunakan untuk menaikkan tingkat energi elektron. Ketika elektron ini kembali ke tingkat energi semula, radiasi tadi dipancarkan kembali. Nilai frekuensi radiasi ini bergantung pada selisih tingkat energi elektron. Karena susunan elektron bersifat khas untuk tiap atom, frekuensi yang diserap dan dipancarkan akan berbeda untuk atom yang berbeda. Yang teramati oleh pengamat yaitu garis-garis terang pada frekuensi tertentu, tanpa disertai kontinum.

Gambar 14. Jika terdapat gas renggang di antara pengamat dan sumber radiasi, terjadi garis-garis serapan. Jika sumber radiasi tidak segaris dengan pengamat dan gas renggang, terjadi garis-garis emisi.

Spektrum energi sumber radiasi berupa spektrum kontinu pada semua panjang gelombang. Jika terdapat gas bertekanan rendah di antara sumber radiasi dan pengamat, radiasi dengan frekuensi tertentu digunakan untuk menaikkan tingkat energi elektron. Ketika elektron ini kembali ke tingkat energi semula, radiasi tadi dipancarkan kembali ke segala arah. Yang teramati oleh pengamat yaitu spektrum kontinu dengan garis gelap pada frekuensi tertentu.

Gambar 15. Nebula planet M 57, yang merupakan lontaran material bintang. Spektrum nebula planet berupa garis-garis terang pada frekuensi tertentu. (AURA/STScI/NASA)

Gambar 16. Korona merupakan gas renggang di antara pengamat dan inti Matahari. Spektrum korona berupa kontinum dengan garis-garis gelap pada frekuensi tertentu. (Luc Viatour)/NASA)

Alat pengurai cahaya disebut spektrograf/spektrometer. Spektrum cahaya dapat direkam dengan, misalnya, kamera digital. Untuk mengetahui frekuensi garis emisi atau serapan, digunakan spektrum pembanding dari percobaan di laboratorium.

Gambar 17. Searah jarum jam dari kiri atas, logam natrium dipanaskan hingga menguap. Gas panas natrium akan memancarkan sinar pada frekuensi tertentu. Sinar ini diuraikan dengan prisma pada spektrograf. Ditampilkan dua garis emisi sampel gas natrium, dilihat dari teropong pada ujung spektrograf. Tentu saja kini, digunakan spektrograf dan perekam data elektronik. (BBC Chemistry: A Volatile History - The Order of the Elements)

Bacaan

Arny, Thomas T. (2004), Explorations: An Introduction to Astronomy, New York, McGraw-Hill
Sutyanto, Winardi (1984), Astrofisika: Mengenal Bintang, Bandung, Penerbit ITB

Bisik-Bisik Gosip Tata Surya

Isi Tata Surya yaitu Matahari, planet, asteroid, komet, planet kerdil, dan benda-benda kecil.

The Small, The Numerous

Menurut aturan Titius-Bode, perbandingan jarak planet dari Matahari mengikuti pola 4, 7, 10, 16, 28, 52, 100, 196, 388, 772. Meskipun tidak ada penjelasan mengapa pola ini berlaku, pola ini memang terjadi pada beberapa planet. Berikut nilai jarak rata-rata planet dari Matahari dan perbandingannya satu sama lain.

Tabel 1. Perbandingan jarak planet dari Matahari.

planet	sumbu semimayor (106 km)	sumbu semimayor (SA)
		pengamatan	Titius-Bode
Merkurius	57,91	0,4	0,4
Venus	108,21	0,7	0,7
Bumi	149,60	1,0	1,0
Mars	227,92	1,5	1,6
Jupiter	778,57	5,2	5,2
Saturnus	1.433,53	9,6	10,0
Uranus	2.872,46	19,2	19,6

Sekali lagi perlu ditegaskan bahwa tidak ada penjelasan mengapa perbandingan jarak planet dari Matahari hampir cocok dengan aturan Titius-Bode. Bagaimanapun, astronom ingin tahu apakah memang aturan Titius-Bode memang berlaku. Jika memang aturan Titius-Bode berlaku, maka di antara Mars dan Jupiter ada planet yang jaraknya sekitar 2,8 SA dari Matahari. Alih-alih menemukan planet, astronom menemukan sabuk asteroid.

Kini, telah diketahui bahwa hanya Merkurius, Venus, Bumi, Mars, Jupiter, Saturnus, Uranus, dan sabuk asteroid saja yang mengikuti aturan Titius-Bode. Benda lain di Tata Surya sama sekali tidak mengikuti aturan tersebut.

Asteroid Belt

Sabuk asteroid dinamai demikian karena isinya bukan benda tunggal, melainkan kumpulan benda yang membentang membentuk daerah mirip sabuk atau cincin. Sabuk asteroid berada di antara orbit Mars dan Jupiter.

Gambar 1. Foto Ceres, asteroid terbesar, diambil dengan teleskop Hubble. (NASA/ESA/J. Parker/P. Thomas/L. McFadden)

Asteroid paling besar dinamai Ceres. Bentuknya bulat, diameternya sekitar 950 km. Ceres juga merupakan asteroid pertama yang ditemukan. Sementara itu, kebanyakan asteroid bentuknya tidak teratur. Bulatnya Ceres terjadi karena cukup besarnya massa Ceres sehingga dapat menarik komponen dirinya membentuk bulatan. Berikut perbandingan massa beberapa asteroid.

Tabel 2. Tahun penemuan dan massa beberapa asteroid.

asteroid	tahun penemuan	massa (1016 kg)	masteroid/mBumi
Ceres	1801	87.000	0,000145641
Pallas	1802	31.800	0,000053234
Vesta	1807	30.000	0,000050221
Hygiea	1849	8.850	0,000014815
Fides	1855	130	0,000000218
Ida	1884	4,2	0,000000007

Umumnya makin kecil massanya, makin sukar suatu benda diamati. Inilah sebabnya makin kecil massa asteroid, makin terlambat dia ditemukan.

Gambar 2. Foto Ida dan satelitnya, Dactyl. Foto diambil dengan wahana Galileo. (NASA/JPL)

Jumlah asteroid sangat banyak. Dapat diperkirakan seberapa rapat sabuk asteroid. Asumsikan bahwa sabuk asteroid tipis, rata-rata orbit asteroid berbentuk lingkaran, dan asteroid tersebar merata! Kemudian, definisikan n jumlah asteroid, d jarak rata-rata antarasteroid, r_o jarak batas luar sabuk asteroid dari Matahari, r_i jarak batas dalam sabuk asteroid dari Matahari, r jarak rata-rata sabuk asteroid dari Matahari, w lebar sabuk asteroid, dan \sigma kerapatan asteroid di sabuk asteroid!

\sigma=\frac{n}{\pi\left(r_o^2-r_i^2\right)}\\\Rightarrow \sigma=\frac{n}{\pi\left(r_o-r_i\right)\left(r_o+r_i\right)}\\\Rightarrow \sigma=\frac{n}{2\pi wr}\cdots\cdots\left(1\right)

Besaran \sigma pada dasarnya menyatakan berapa banyak asteroid per luas area. Jadi, 1/\sigma menyatakan berapa luas area yang ditempati tiap asteroid.

Gambar 3. Ilustrasi asumsi daerah yang ditempati tiap asteroid di sabuk asteroid. Ditunjukkan juga dua kemungkinan besar jarak sebuah asteroid ke asteroid terdekat.

Berikut jarak rata-rata antarasteroid.

d=\frac{4d_1+4d_2}{8}\\\Rightarrow d=\frac{1}{2}\left(\frac{1+\sqrt{2}}{\sqrt{\sigma}}\right)\\\Rightarrow d=\frac{2+\sqrt{2}}{2}\sqrt{\frac{\pi rw}{n}}\cdots\cdots\left(2\right)

Gambar 4. Ilustrasi sebaran asteroid di sabuk asteroid pada 14 Agustus 2006, ditandai sebagai titik-titik putih, dilihat tegak lurus bidang ekliptika. (NASA/JPL/Minor Planet Center)

Dapat dilihat pada gambar di atas bahwa lebar sabuk asteroid kira-kira sama dengan radius orbit Bumi. Jadi, r\approx 2,8\cdot 150.000.000 \text{ km} dan w\approx 150.000.000 \text{ km}. Dua nilai ini dimasukkan ke (2) sehingga didapat hubungan berikut.

\\d\approx \frac{759.461.738}{\sqrt{n}} \text{ km}\cdots\cdots\left(3\right)

Jika dianggap terdapat sejuta asteroid, berikut jarak rata-rata antarasteroidnya.

\\d\approx \frac{759.461.738}{\sqrt{1.000.000}} \text{ km}\approx 759.462 \text{ km}\cdots\cdots\left(4\right)

Jadi jika ada sejuta asteroid, maka jarak rata-rata antarasteroid hampir dua kali jarak Bumi-Bulan. (Jarak rata-rata Bumi-Bulan sekitar 384.0000 km.) Pada jarak sebesar ini, berikut diameter sudut Ceres.

\\\theta_{Ceres}\approx 2 \arctan\left(\frac{\tfrac{1}{2}\cdot 950 \text{ km}}{759.461 \text{ km}}\right)\approx 0,07^\circ\cdots\cdots\left(5\right)

Dengan demikian jika dianggap sabuk asteroid tipis, sebarannya merata, dan orbit asteroid berupa lingkaran, maka dari asteroid lain, Ceres tampak sekitar sepuluh kali lebih kecil dari ukuran Bulan. (Diameter sudut Bulan sekitar 0,5°.)

Perkiraan tadi menggunakan asumsi sabuk asteroid tipis. Kenyataannya, sabuk asteroid memiliki ketebalan yang seharusnya dipertimbangkan dalam perhitungan. Dampaknya yaitu asteroid lebih tersebar karena lebih banyak ruang yang dapat ditempati. Tidaklah aneh jika belum pernah ada wahana luar angkasa yang menabrak asteroid ketika melewati sabuk asteroid.

Trojan Swarm

Sekitar seratus tahun setelah Ceres ditemukan, ditemukan kumpulan asteroid yang mengiringi Jupiter. Kumpulan ini dinamai asteroid Trojan. Sebarannya pada 14 Agustus 2006 dapat dilihat pada gambar 4, ditandai sebagai titik-titik hijau.

Pada sistem tiga benda, terdapat lima lokasi di sekitar mereka yang besar gaya gravitasinya sama dengan besar gaya sentripetalnya. Lokasi ini dinamai titik Lagrange. Tiga titik Lagrange berada segaris dengan garis hubung pusat massa dua benda, sementara dua titik lainnya membentuk segitiga sama sisi yang alasnya garis hubung dua benda.

Telah ditemukan juga asteroid Trojan yang mengiringi Mars dan Neptunus.

Gambar 5. Ilustrasi posisi titik Lagrange sistem tiga benda.

Close and Dangerous

Ada juga asteroid yang orbitnya dekat atau memotong orbit Bumi. Asteroid ini dinamai Near Earth Asteroid (NEA). Dengan demikian jika dulu dikatakan bahwa asteroid berada di sabuk asteroid, kini dikatakan bahwa ada asteroid yang di sabuk asteroid, ada yang mengiringi Jupiter, Mars, dan Neptunus, dan ada yang di sekitar Bumi.

Daerah Tata Surya Dalam lebih rapat daripada Tata Surya Luar karena lebih banyak planet untuk luas area tertentu. Dampaknya yaitu usikan gravitasi di Tata Surya Dalam sering terjadi. Jadi, orbit NEA tidak akan berumur panjang. Seiring waktu, orbitnya akan berubah akibat usikan gravitasi dari planet dalam. Asal NEA mungkin dari sabuk asteroid atau daerah tertentu yang mendapat usikan gravitasi Jupiter, planet termasif di Tata Surya.

Gambar 6. Ilustrasi orbit NEA Atira, Aten, Apollo, dan Amor.

Ditinjau dari orbitnya, ada empat kelompok NEA. (Besaran a yaitu sumbu semimayor, Q yaitu aphelion, dan q yaitu perihelion.)

1. Atira. Orbit asteroid ini berada di dalam orbit Bumi, a < 1 SA, Q < 0,983 SA.
2. Aten. Orbit asteroid ini memotong orbit Bumi, namun sumbu semimayornya lebih pendek dari sumbu semimayor orbit Bumi, a < 1 SA, Q > 0,983 SA.
3. Apollo. Orbit asteroid ini memotong orbit Bumi dan sumbu semimayornya lebih panjang dari sumbu semimayor orbit Bumi, a > 1 SA, q < 1,017 SA.
4. Amor. Orbit asteroid Amor hampir selalu berada di antara Bumi dan Mars, a > 1 SA, 1,017 SA < q < 1,3 SA.

Celestial Tailed Beast

Komet juga merupakan anggota Tata Surya. Pun komet beredar mengelilingi Matahari. Ketika mendekati Matahari, bahan pada komet dipanasi Matahari dan menguap.

Rata-rata ukuran dan massa komet lebih kecil dari rata-rata ukuran dan massa asteroid. Intinya tersusun atas batuan, debu, bekuan air, dan bekuan gas. Karena massanya kecil, bentuk inti komet tidak teratur. Jika hanya inti saja yang teramati, maka komet hampir tidak dapat dibedakan dari asteroid.

Gambar 7. Potret komet Halley, 29 Mei 1910. (The Yerkes Observatory)

Komet berasal dari luar orbit Neptunus. Jauhnya jarak daerah ini dari Matahari memungkinkan bahan-bahan pada komet tetap beku. Karena usikan gravitasi planet-planet jovian atau bintang yang melintas dekat Tata Surya, orbit komet berubah sedemikian sehingga lintasannya masuk ke daerah Tata Surya Dalam.

Di Tata Surya Dalam, radiasi Matahari menguapkan bekuan pada komet. Aliran uap ini membawa serta debu. Jika gaya gravitasi inti komet sanggup menahan uap dan debu ini, terbentuk selubung uap dan debu yang disebut koma.

Gambar 8. Inti komet Tempel 1, dipotret dengan wahana Deep Impact. (NASA/JPL/Caltech/UMD)

Radiasi Matahari memiliki tekanan. Selain itu, Matahari juga memancarkan angin Matahari, yang isinya ion. Baik tekanan radiasi maupun angin Matahari mendorong koma sehingga terulur membentuk ekor. Ekor komet dapat membentang hingga sejauh 1 SA dari inti komet.

Seperti koma, ekor komet terdiri atas debu dan gas. Rata-rata massa debu lebih besar dari rata-rata massa gas. Jadi, pengaruh tekanan radiasi dan angin Matahari pada debu lebih kecil dari pengaruhnya pada gas. Debu yang terlontar dari inti komet akan tertinggal, membentuk ekor debu yang melengkung. Sementara itu, tekanan radiasi dan angin Matahari selalu mengarah menjauhi Matahari. Akibatnya yaitu ekor gas komet selalu lurus dan menjauhi Matahari.

Gambar 9. Ekor debu dan gas komet. Ekor gas selalu menjauhi Matahari, sementara ekor debu selalu terseret, melengkung menjauhi arah gerak komet. (NASA Ames Researh Center/K. Jobse/P. Jenniskens)

Kebanyakan komet memiliki orbit yang sangat lonjong. Berdasarkan orbitnya, komet dibagi menjadi kelompok-kelompok berikut.

1. Komet Periode Pendek. Komet ini memiliki periode kurang dari 200 tahun. Komet periode pendek dibagi lagi menjadi dua kelompok, yakni komet keluarga Jupiter (JFC, Jupiter Family Comet), jika periodenya kurang dari 20 tahun, dan komet keluarga Halley (HFC, Halley Family Comet), jika periodenya antara 20 dan 200 tahun.
2. Komet Periode Panjang. Komet ini memiliki periode lebih dari 200 tahun.
3. Komet Penampakan Tunggal. Komet ini memiliki lintasan berupa parabola atau hiperbola. Dua jenis lintasan ini bukan lintasan tertutup sehingga bisa saja komet ini kemudian lepas dari Tata Surya. Walaupun demikian ketika di Tata Surya Dalam, komet ini belum tentu lepas. Ini karena usikan gravitasi planet jovian dapat menjadikan lintasan komet tersebut elips.
4. Komet Sabuk Asteroid. Telah ditemukan adanya komet di sabuk asteroid. Penemuan komet ini mengaburkan perbedaan antara asteroid dan komet. Boleh jadi komet merupakan asteroid yang memiliki bahan mudah menguap, atau boleh jadi asteroid merupakan komet yang tidak aktif.

Dari Hukum III Kepler, dapat ditentukan panjang sumbu semimayor orbit jika diketahui kala revolusi.

\frac{T_{komet}^2}{a_{komet}^3}=\frac{T_{Bumi}^2}{a_{Bumi}^3}=1 \text{ tahun}^2/\text{SA}^3\\\Rightarrow a_{komet}=\left(\frac{T_{komet}^2}{1 \text{ tahun}^2}\right)^{1/3} \text{SA}\cdots\cdots\left(6\right)

Dari persamaan (6), dapat ditentukan panjang sumbu semimayor orbit komet.

Tabel 3. Panjang sumbu semimayor komet.

kelompok asteroid	sumbu semimayor
JFC	< 7,4 SA
HFC	7,4-34,2 SA
periode panjang	> 34,2 SA

Tentu saja bentuk dan orientasi orbit komet beragam dan tidak tetap, tergantung eksentrisitas, sudut kemiringannya terhadap ekliptika, dan usikan gravitasi Neptunus, Uranus, Saturnus, dan, terutama, Jupiter.

Yet Another Belt

Tahun 1943, Kenneth Essex Edgeworth mengajukan hipotesis keberadaan benda-benda kecil di luar orbit Neptunus. Hipotesis serupa juga diajukan oleh Gerard Kuiper pada tahun 1951.

Hipotesis ini didukung oleh kondisi fisik komet. Ketika dekat dengan Matahari, bahan inti komet menguap. Padahal, usia Tata Surya 4,5 milyar tahun. Rentang waktu ini tentu cukup untuk menguapkan seluruh bahan inti komet. Kenyataannya, penampakan koma dan ekor komet masih saja ada hingga kini. Jadi, mungkin saja ada daerah di luar orbit Neptunus yang isinya benda-benda kecil dan inti komet. Dari daerah inilah mungkin komet berasal. Penampakan koma dan ekor terjadi ketika komet ditarik ke Tata Surya Dalam oleh planet jovian. Daerah asal komet periode pendek dinamai sabuk Kuiper, sementara daerah asal komet periode panjang dinamai awan Oort.

Gambar 10. Sebaran benda-benda di sabuk Kuiper pada 1 Januari 2000, ditandai sebagai titik-titik hijau. Matahari dan planet-planet jovian diberi label nama. (Minor Planet Center)

Tahun 1992, David Jewitt dan Jane Luu berhasil mendeteksi keberadaan dua benda di daerah sabuk Kuiper. Kini, telah dideteksi keberadaan puluhan benda di sabuk Kuiper.

Pluto merupakan anggota sabuk Kuiper. Meskipun demikian ketika Pluto ditemukan, keberadaan sabuk Kuiper tidak dapat dipastikan.

Dwarf Members Rise

Ketika Pluto ditemukan tahun 1930, telah diketahui keberadaan Matahari, komet, asteroid, dan tentu saja planet. Dibandingkan planet, orbit Pluto sangat lonjong. Pun orbitnya memotong orbit Neptunus. Bagaimanapun, Pluto berbentuk bundar dan orbitnya bersih dari benda lain. (Ceres juga bundar, namun di sekelilingnya banyak asteroid lain.) Karena itu, Pluto dikelompokkan sebagai planet.

Tahun 1990-an, telah ditemukan benda-benda di daerah sabuk Kuiper. Benda-benda ini memiliki orbit serupa Pluto, yakni sangat lonjong dan tidak sebidang dengan ekliptika. Astronom mulai curiga bahwa Pluto merupakan bagian dari kelompok tersendiri yang menghuni sabuk Kuiper.

Tahun 2005, telah diketahui keberadaan Quaoar, Sedna, dan Eris. Ukuran ketiganya tidak jauh berbeda dengan Pluto, pun orbitnya juga lonjong dan tidak sebidang dengan ekliptika. Akhirnya pada tahun 2006, International Astronomical Union (IAU) menetapkan definisi-definisi berikut untuk anggota Tata Surya.

1. Planet. Planet yaitu benda langit yang a) orbitnya mengelilingi Matahari, b) massanya cukup besar sehingga bentuknya hampir bulat, dan c) telah membersihkan orbitnya dari benda-benda lain.
2. Planet Kerdil. Planet kerdil yaitu benda langit yang a) orbitnya mengelilingi Matahari, b) massanya cukup besar sehingga bentuknya hampir bulat, c) belum membersihkan orbitnya dari benda-benda lain, dan d) bukan satelit.
3. Benda Kecil. Benda kecil yaitu benda-benda selain planet, planet kerdil, atau satelit.

Dalam definisi IAU di atas, satelit yaitu benda yang mengelilingi benda lain selain Matahari, yang pusat massa sistemnya di bawah permukaan benda yang dikelilingi. Sementara itu, maksud membersihkan orbitnya yaitu massanya dominan sehingga sekalipun ada benda-benda lain di orbitnya, mereka di bawah pengaruh gravitasi massa dominan tersebut. Dengan demikian, Jupiter merupakan planet karena kumpulan asteroid di orbitnya terikat gravitasi Jupiter, sementara Ceres bukan planet karena pengaruh gravitasinya pada asteroid lain tidak dominan.

Melalui spektroskopi, diketahui bahwa kebanyakan benda di sabuk Kuiper tersusun terutama atas bekuan air dan senyawa hidrokarbon.

Story of Pluto

Tahun 1906, Percival Lowell mengadakan pencarian planet kesembilan. Hingga meninggalnya, Percival Lowell tidak menemukannya.

Tahun 1929, Vesto Melvin Slipher, kepala observatorium yang didirikan Lowell, menugaskan pencarian planet kesembilan pada Clyde Tombaugh. Setelah setahun mencari objek yang perpindahan posisinya besar pada plat-plat foto, Tombaugh menemukan planet kesembilan. Nama "Pluto" diusulkan oleh Venetia Burney, siswa sekolah dasar di Inggris.

Gambar 11. Dua dari sekian banyak plat foto yang diperiksa Clyde Tombaugh. Yang dicari yaitu objek yang pergeserannya besar. Pada gambar, objek tersebut ditandai dengan tanda panah; itulah Pluto. (Lowell Observatory Archives)

Tahun 1978, James W. Christy memeriksa kembali plat-plat foto Pluto. Dia menemukan bahwa foto Pluto lonjong pada sejumlah plat. Ternyata, periode kelonjongan foto Pluto sama dengan periode rotasi Pluto. Disimpulkan bahwa ada benda lain yang mengorbit Pluto, dengan periode revolusi sama dengan periode rotasi Pluto.

Gambar 12. Dua dari plat-plat foto yang diperiksa James W. Christy pada tahun 1978. Foto kiri lebih lonjong dari foto kanan. (United States Naval Observatory)

Tahun 1985, dipastikan bahwa memang ada benda yang mengorbit Pluto. Satelit Pluto ini dinamai Charon. Akhirnya pada tahun 2005, ditemukan lagi dua satelit Pluto, yakni Nix dan Hydra.

Pluto's New Home

Pluto mengelilingi Matahari dan bentuknya hampir bulat. Sementara itu sejak 1985, diketahui bahwa lingkungan Pluto ditempati oleh banyak benda yang tidak banyak terpengaruh gravitasi Pluto. Jadi, Pluto belum membersihkan orbitnya. Sejak 2006, Pluto dinyatakan sebagai planet kerdil.

Gambar 13. Pluto dan tiga satelitnya, dipotret dengan teleskop Hubble. (H. Weaver/A. Stern/HST Pluto Companion Search Team)

Pun status Charon sebagai satelit dipertanyakan. Jika m yaitu massa dan d jarak pisah Pluto-Charon diukur dari Pluto, dapat dihitung C, jarak pusat massa Pluto-Charon dari Pluto.

C=\frac{m_{Pluto}\cdot 0+m_{Charon}\cdot d}{m_{Pluto}+m_{Charon}}\\\Rightarrow C=\frac{m_{Charon}}{m_{Pluto}+m_{Charon}}d\cdots\cdots\left(7\right)

Diketahui massa Pluto 1,31.10²² kg dan massa Charon 1,52.10²¹ kg.

C=\frac{1,52\cdot 10^{21} \text{ kg}}{1,31\cdot 10^{22} \text{ kg}+1,52\cdot 10^{21} \text{ kg}}d\\\Rightarrow C=0,104\cdot d\cdots\cdots\left(8\right)

Jadi, pusat massa Pluto-Charon selalu terletak pada sekitar 1/10 jarak pisah Pluto-Charon. Sementara itu, diketahui jarak rata-rata Charon-Pluto yaitu 19.600 km. Dapat dihitung jarak pusat massa Pluto-Charon dari pusat massa Pluto.

\\C=0,104\cdot 19.600 \text{ km} = 1.960 \text{ km}\cdots\cdots\left(9\right)

Gambar 14. Posisi pusat massa Pluto-Charon berada di atas permukaan Pluto. Jadi, Pluto dan Charon saling mengelilingi.

Padahal, jari-jari Pluto 1.195 km. Jadi, pusat massa Pluto-Charon selalu di atas permukaan Pluto. Dengan demikian, dapat dianggap bahwa Pluto-Charon merupakan sistem planet kerdil ganda.

Yet Another Further, Bigger Swarm

Tahun 1932 untuk menjelaskan keberadaan komet periode panjang, Ernst Öpik mengajukan hipotesis keberadaan kumpulan inti komet di bagian luar Tata Surya, lebih jauh daripada sabuk Kuiper. Tahun 1950, Jan Hendrik Oort mengajukan hipotesis serupa.

Gambar 15. Ilustrasi perbandingan ukuran awan Oort terhadap sabuk Kuiper dan orbit Pluto. (NASA/JPL)

Benda-benda di awan Oort kebanyakan tersusun atas bekuan air dan gas. Meskipun demikian pada tahun 1996, ditemukan asteroid yang menghuni awan Oort. Ada juga planet kerdil di awan Oort, yang ditemukan tahun 2003 dan dinamai Sedna.

Gambar 16. Perbandingan ukuran Tata Surya Dalam, Tata Surya Luar, orbit Sedna, dan awan Oort. (NASA/JPL-Caltech/R. Hurt)

Bacaan

Buie, Marc W., William M. Grundy, Eliot F. Young, Leslie A. Young, dan S. Alan Stern (2006), Orbits and Photometry of Pluto's Satellites: Charon, S/2005 P1, and S/2005 P2, The Astronomical Journal 132: 290-298
Nicholson, Seth B. (1961), The Trojan Asteroids, Astronomical Society of the Pacific, Leaflet No. 381
Person, M.J., A.A.S. Gulbis, J.M. Pasachoff, B.A. Babcock, S.P. Souza, dan J. Gangestad (2006), Charon's Radius and Density from the Combined Data Sets of the 2005 July 11 Occultation, The Astronomical Journal 132: 1575-1580
Weissman, Paul R. dan Harold F. Levison (1997), Origin and Evolution of the Unusual Object 1996 PW: Asteroids from the Oort Cloud, The Astrophysical Journal 488: L133-L136

Pak Kepler dan Pak Newton

Materi ini ditulis bersama dengan Dra. Etty Jaskarti, M.Pd.

Laju revolusi planet tidak tetap. Di dekat perihelion, kelajuan planet lebih besar daripada di dekat aphelion. Laju orbit dan kala revolusi planet dijelaskan dengan Hukum Kepler.

Pada abad 2, Claudius Ptolomeus merumuskan teori geosentris, yaitu model Bumi sebagai pusat alam semesta dan planet-planet bergerak melingkar mengelilingi Bumi. Pada abad 16, Copernicus (1473-1543) mengajukan kembali teori heliosentris, dengan Matahari sebagai pusat Tata Surya dan planet-planet beredar mengelilinginya.

Pertentangan kedua teori tadi mendorong para ahli mengumpulkan data pengamatan, seperti yang dilakukan oleh Tycho Brahe (1546-1601). Data gerak planet dari pengamatan Tycho Brahe dianalisis selama kurang lebih 20 tahun oleh Johannes Kepler (1571-1630). Kesimpulan Kepler dituangkan dalam ketiga hukumnya tentang gerak planet.

Kepler's Laws

Berikut Hukum I Kepler.

"Semua planet bergerak dalam lintasan elips dan Matahari terletak pada salah satu fokusnya."

Dalam lintasan elips, ada posisi terdekat dan terjauh dari titik fokusnya. Elips adalah suatu kurva tertutup sedemikian sehingga jumlah jarak dari sembarang titik ke kedua titik fokusnya tetap. Definisi ini diilustrasikan dalam gambar di bawah.

Gambar 1. Kurva elips. Definisi elips yaitu kumpulan titik, atau kurva, yang jumlah jaraknya dari kedua fokus selalu tetap; F₁P₁ + F₂P₁ = F₁P₂ + F₂P₂.

Berikut Hukum II Kepler.

"Setiap planet bergerak sedemikian sehingga suatu garis khayal yang ditarik dari Matahari ke planet tersebut akan menyapu luas yang sama dalam selang waktu yang sama."

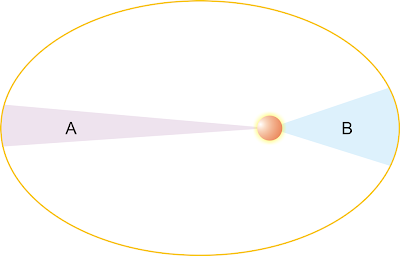Gambar 2. Jika sebuah planet yang mengorbit Matahari menyapu daerah A dan B yang luasnya sama, maka waktu tempuh sapuannya juga sama. Ini berarti kelajuan ketika menyapu A lebih kecil dari ketika menyapu B.

Berikut Hukum III Kepler.

"Kuadrat kala revolusi planet sebanding dengan pangkat tiga jarak rata-rata planet tersebut ke Matahari."

Jika T periode dan R rata-rata jarak ke Matahari, berlaku rumusan berikut.

\\\frac{T^2}{R^3}=\text{konstan}\cdots\cdots\left(1\right)

Untuk dua planet, berlaku hubungan berikut.

\\\frac{T_1^2}{R_1^3}=\frac{T_2^2}{R_2^3}\cdots\cdots\left(2\right)

Hukum Kepler merupakan dukungan kuat untuk teori Copernicus. Meski demikian, Kepler tidak memiliki konsep gaya sebagai penyebab berlakunya kesimpulannya. Newtonlah yang berhasil menurunkan Hukum Kepler dari Hukum Gravitasi Universal yang digagasnya. (Lihat alur pemikiran penurunan Hukum Kepler dari Hukum Gerak Newton dan Hukum Gravitasi Universal di Gara-Gara Gravitasi.)

Hukum Gravitasi Universal mengharuskan setiap planet ditarik menuju Matahari dengan sebuah gaya yang berbanding terbalik dengan kuadrat jarak dari Matahari. Dengan gagasan ini, Newton mampu menerangkan gerak planet di Tata Surya dan gerak jatuh di dekat permukaan Bumi dengan satu konsep saja. Dengan kata lain, Newton berhasil menyatukan mekanika benda langit dan mekanika kebumian, yang sebelumnya dua kajian terpisah.

Undisputed Universality

Sebelumnya, Galileo telah mempelajari gerak benda di Bumi dan Kepler telah menyatakan tiga hukum yang menggambarkan gerakan planet. Kajian keduanya dilanjutkan oleh Newton, yang berusaha menjelaskan gerakan benda di Bumi dan gerakan planet. Akhirnya, Newton memperoleh rumusan yang mendeskripsikan mekanisme umum pergerakan segala benda.

Newton memikirkan kasus benda jatuh. Karena setiap benda jatuh mengalami percepatan, Newton menyimpulkan bahwa terdapat gaya yang bekerja pada benda tersebut. Gaya ini disebut gaya gravitasi. Pertanyaannya yaitu bagaimana gaya ini bekerja pada. Jika pada benda bekerja suatu gaya maka gaya itu tentu saja berasal dari benda lain. Karena setiap benda yang dilepaskan selalu jatuh ke Bumi, Newton menganggap bahwa Bumi sendiri yang melakukan gaya pada setiap benda. Arah gaya gravitasi ini selalu menuju pusat Bumi.

Jika gaya gravitasi Bumi bekerja pada puncak pohon dan juga pada puncak gunung, tentu gaya ini juga bekerja pada Bulan dan juga bekerja pada benda-benda langit. Berdasarkan inspirasi ini, dan dengan bantuan dan dorongan yang kuat dari Robert Hooke (1635-1703), Newton kemudian membangun Hukum Gravitasi Universal.

Dari hasil pekerjaan Galileo dan ilmuwan lainnya, Newton mengetahui bahwa percepatan benda yang jatuh bebas dekat permukaan Bumi yaitu 9,8 m/s² ke arah pusat Bumi. Selanjutnya, Newton membandingkan percepatan sentripetal bulan yang bergerak mengelilingi Bumi dan percepatan gravitasi di permukaan Bumi. Newton mengetahui bahwa Bulan mempunyai percepatan yang arahnya ke Bumi dan orbit yang hampir melingkar. Percepatan ini disebabkan oleh suatu gaya dari Bumi, yang secara kontinu menarik Bulan. Inilah gaya gravitasi, gaya yang sama dengan yang menarik apel jatuh ke Bumi. Tapi apakah gaya tarik ini sama untuk Bulan, yang jaraknya lebih jauh dari permukaan Bumi, dan apel? Apakah lebih kuat atau lebih lemah?

Mula-mula, Newton mencari kelajuan Bulan mengelilingi Bumi. Rata-rata jarak orbit Bulan yaitu 384.000 km. Untuk sekali mengorbit Bumi, dibutuhkan waktu bagi Bulan sebanyak 27,3 hari. Dapat dihitung bahwa kelajuan Bulan mengelilingi Bumi besarnya 1.033,75 m/s. Dapat dihitung pula bahwa percepatan sentripetal Bulan menuju Bumi.

a_{sp}=\frac{v^2}{R}\\\Rightarrow a_{sp}=\left(\frac{2 \pi R}{T}\right)^2 \frac{1}{R}\\\Rightarrow a_{sp}=\tfrac{4 \pi^2}{T^2}R\\\Rightarrow a_{sp}=2,72\cdot 10^{-3}\text{ m/s}^2\cdots\cdots\left(3\right)

Percepatan gravitasi di permukaan Bumi besarnya 9,8 m/s². Berikut perbandingan antara percepatan ke pusat Bumi pada orbit Bulan dan pada permukaan Bumi.

\\\frac{a_{sp}}{g}=\frac{2,72\cdot 10^{-3}\text{ m/s}^2}{9,8\text{ m/s}^2}\approx\frac{1}{3.600}\cdots\cdots\left(4\right)

Inilah percepatan Bulan menuju Bumi, yaitu kira-kira 1/3.600 kali percepatan gravitasi di permukaan Bumi. Jarak Bumi-Bulan, atau jari-jari orbit Bulan mengelilingi Bumi, yaitu 384.000 km, sedangkan jari-jari Bumi sekitar 6.380 km.

\\\frac{d_{Bumi-Bulan}}{R_{Bumi}}\approx 60\cdots\cdots\left(5\right)

Jadi, ada kemungkinan gaya tarik ke Bumi, yang sebanding dengan percepatannya ke Bumi, berbanding terbalik dengan kuadrat jaraknya dari pusat Bumi.

\\F\propto \frac{1}{R^2}\cdots\cdots\left(6\right)

Jika memang ini yang terjadi, Bulan yang jauhnya 60 kali jari-jari Bumi merasakan gaya gravitasi sebesar 1/3600 kali gaya gravitasi di permukaan Bumi. Lebih jauh lagi, setiap benda yang ditempatkan sejauh 384.000 km dari pusat Bumi akan mengalami percepatan gravitasi sebesar yang dialami Bulan, yakni 0,00272 m/s².

Newton menyadari bahwa gaya gravitasi pada benda tidak hanya bergantung pada jaraknya dari pusat Bumi, tetapi juga pada massanya. Menurut Hukum III Gerak Benda, ketika Bumi melakukan gaya gravitasi pada benda, Bulan misalnya, benda itu juga melakukan gaya reaksi pada Bumi. Besar kedua gaya tersebut sama tetapi arahnya berlawanan.

Akhirnya, Newton mengemukakan bahwa besarnya gaya gravitasi berbanding lurus dengan massa kedua benda.

\\F\propto \frac{Mm}{R^2}\cdots\cdots\left(7\right)

Dalam hubungan di atas, M yaitu massa Bumi, m yaitu massa benda, dan R yaitu jarak antara pusat Bumi dan benda.

Newton melangkah lebih jauh dalam menganalisis gravitasi. Dalam kajiannya tentang orbit planet, ia menyimpulkan bahwa gaya yang diperlukan untuk mempertahankan planet-planet itu bergerak mengelilingi Matahari juga berkurang, berbanding terbalik dengan kuadrat jaraknya terhadap Matahari. Hal itu membuatnya semakin yakin bahwa gravitasilah yang bekerja pada Matahari dan planet-planet sehingga setiap planet tetap pada orbitnya. Jika gaya gravitasi bekerja pada benda-benda ini, mengapa tidak sekalian bekerja pada semua benda? Pemikiran inilah yang mendasari dirumuskannya Hukum Gravitasi Universal.

Setiap benda di alam semesta menarik benda lain dengan suatu gaya yang besarnya sebanding dengan hasil kali kedua massa benda dan berbanding terbalik dengan kuadrat jarak antara keduanya. Gaya ini bekerja sepanjang garis yang menghubungkan kedua benda itu.

Secara matematis, besarnya gaya gravitasi dapat ditulis sebagai berikut.

\\F_{1,2}=F_{2,1}=G\frac{m_1 m_2}{R^2}\cdots\cdots\left(8\right)

Besaran m_1 dan m_2 yaitu massa masing-masing benda, R yaitu jarak antara dua benda, dan G yaitu tetapan yang nilainya ditentukan melalui eksperimen.

Gaya gravitasi antara dua benda pertama kali diukur oleh Henry Cavendish pada tahun 1798, lebih dari seratus tahun setelah diterbitkannya hukum-hukum Newton. Dalam eksperimennya, ia menggunakan peralatan yang dibuatnya sendiri, sebagaimana yang ditunjukkan pada gambar.

Gambar 3.Instrumen dalam eksperimen Cavendish. (Henry Cavendish)

Pada peralatan Cavendish, dua bola ditempatkan pada ujung-ujung tongkat horizontal yang digantung pada pusatnya dengan seutas benang halus. Bila bola ketiga didekatkan ke salah satu benda yang digantung, gaya gravitasi menyebabkan bola yang digantung bergerak. Hal ini akan memuntir benang. Pergerakan yang kecil ini selanjutnya diperjelas menggunakan berkas cahaya, yang diarahkan ke cermin. Berkas cahaya ini kemudian memantul dan menimpa skala. Penentuan besarnya gaya yang memuntir benang selanjutnya memungkinkan penentuan besarnya gaya gravitasi antara dua benda.

Cavendish tidak hanya memperkuat temuan Newton bahwa dua buah benda saling tarik-menarik, tetapi ia juga dapat mengukur besarnya gaya tarik kedua bola, massa masing-masing bola, dan jarak pisahnya sehingga dapat diperoleh nilai tetapan gravitasi. Berikut nilai tetapan gravitasi.

\\G=6,67\cdot 10^{-11}\text{ Nm}^2 \text{kg}^{-2}\cdots\left(9\right)

Gravity In Action

Hukum Kepler dan Hukum Gravitasi Universal memungkinkan diketahuinya besaran-besaran pada anggota Tata Surya. Tinjaulah kasus berikut!

Bumi bergerak mengelilingi Matahari dalam orbit yang berbentuk hampir lingkaran. Dengan demikian, pada Bumi bekerja gaya sentripetal F_{sp}. Gaya ini berasal dari Matahari.

\sum F=F_{sp}\\ \Rightarrow F_g=F_{sp}\\ \Rightarrow G\frac{Mm}{R^2}=m\frac{v^2}{R}\cdots\cdots\left(10\right)

Sementara itu, v=2\pi R/T. Diketahui kala revolusi Bumi 3,15.10⁷ s dan jarak Bumi-Matahari yaitu 1,5.10¹¹ m. Dari data ini, dapat dihitung besar massa Matahari.

M_{Mat}=\left(\frac{2\pi R}{T}\right)^2=\frac{4\pi^2 R^3}{T^2 G}\\\Rightarrow M_{Mat}=\frac{4\pi^2\left(1,5\cdot 10^{11}\right)^3}{\left(3,15\cdot 10^7\right)^2 6,67\cdot 10^{-11}}\text{ kg} \\ \Rightarrow M_{Mat}=2,01\cdot 10^{30}\text{ kg} \cdots\cdots\left(11\right)

Gaya gravitasi merupakan besaran vektor sehingga penjumlahannya harus menggunakan kaidah penjumlahan vektor. Gambar menunjukkan sebuah benda yang massanya m_1 dipengaruhi oleh benda yang massanya m_2 dan m_3. Akibatnya pada benda m_1, bekerja gaya F_{1,2}, yaitu interaksi antara m_1 dan m_2, serta F_{1,3}, yaitu interaksi antara m_1 dan m_3. Berikut resultan gaya gravitasi yang bekerja pada m_1.

Gambar 4. Benda m₁ dipengaruhi gravitasi m₂ dan m₃.

\\\vec{F_1}=\vec{F_{1,2}}+\vec{F_{1,3}}\cdots\cdots\left(12\right)

Besar resultan gayanya dihitung dengan aturan penjumlahan vektor.

\\F_1^2=F_{1,2}^2+F_{1,3}^2+2F_{1,2}F_{1,3}\cos\alpha\cdots\cdots\left(13\right)

Tinjaulah kasus ketika posisi Matahari, Bumi, dan Bulan membentuk sudut siku-siku pada Bulan! Dapat dihitung gaya gravitasi pada Bulan untuk kasus ini.

Gambar 5. Susunan ketika Bumi, Bulan, dan Matahari membentuk sudut siku-siku pada Bulan.

Diketahui massa Bulan 7,35.10²² kg, massa Bumi 5,89.10²⁴ kg, massa Matahari 1,99.10³⁰ kg, jarak Bumi-Bulan 3,84.10⁸ m, dan jarak Bulan-Matahari 1,50.10¹¹ m. Berikut gaya gravitasi Bulan-Bumi.

F_{Bulan,Bumi}=G\frac{m_{Bulan}m_{Bumi}}{R_{Bulan,Bumi}^2}\\\Rightarrow F_{Bulan,Bumi}=1,96\cdot 10^{20}\text{ N}\cdots\cdots\left(14a\right)

Berikut gaya gravitasi Bulan-Matahari.

F_{Bulan,Matahari}=G\frac{m_{Bulan}m_{Matahari}}{R_{Bulan,Bumi}^2}\\\Rightarrow F_{Bulan,Matahari}=4,34\cdot 10^{20}\text{ N}\cdots\cdots\left(14b\right)

Karena gaya gravitasi pada Bulan dari Matahari dan Bumi saling tegak lurus, berikut resultan gaya pada Bulan.

F_{Bulan}=\sqrt{F_{Bulan,Matahari}^2+F_{Bulan,Bumi}^2}\\\Rightarrow F_{Bulan}=\sqrt{\left(1,96\cdot 10^{20}\right)^2+\left(4,34\cdot 10^{20}\right)^2}\text{ N} \\\Rightarrow F_{Bulan}=4,76\cdot 10^{20}\text{ N} \cdots\cdots\left(15\right)

Berikut sudut antara gaya resultan dan F_{Bulan,Bumi}.

\theta=\tan^{-1}\left(\frac{F_{Bulan,Matahari}}{F_{Bulan,Bumi}}\right) \\ \Rightarrow \theta=\tan^{-1}\left(\frac{4,34\cdot 10^{20}}{1,96\cdot 10^{20}}\right)=65,70^\circ\cdots\cdots\left(16\right)

On The Surface

Gaya gravitasi pada benda-benda di permukaan Bumi tidak lain merupakan berat benda. Jadi, mg=G\tfrac{Mm}{R^2} sehingga g=G\tfrac{M}{R^2}.

Percepatan gravitasi Bumi ditentukan oleh massa Bumi dan jaraknya dari pusat Bumi. Jika diketahui percepatan gravitasi di permukaan Bumi 9,8 m/s² dan jari-jari Bumi 6,38.10⁶ m, dapat ditentukan massa Bumi.

\\M_{Bumi}=\frac{g_{Bumi}}{G}R_{Bumi}^2=5,98\cdot 10^{24}\text{ kg}\cdots\cdots\left(17\right)

Dapat pula dihitung percepatan gravitasi di permukaan planet lain.

\\g_{planet}=G\frac{M_{planet}}{R_{planet}^2}\cdots\cdots\left(18\right)

Bentuk Bumi bukan bulat sempurna, tetapi agak pepat pada kedua kutubnya. Oleh karena itu, jari-jari Bumi berbeda-beda dari satu tempat ke tempat lain. Perbedaan jari-jari Bumi mengakibatkan perbedaan nilai g di permukaan Bumi. Tempat yang jari-jarinya lebih kecil percepatan gravitasinya lebih besar dari tempat yang jari-jarinya lebih besar.

Tabel 1. Percepatan gravitasi di atas permukaan Bumi.

ketinggian (km)	percepatan gravitasi (m/s2)
1	9,80
10	9,77
1.000	7,32
2.000	5,68
3.000	4,35
4.000	3,70
5.000	3,08
6.000	2,60
7.000	2,23
8.000	1,93
9.000	1,69
10.000	1,49
50.000	0,13
∞	0,00

Tabel 2. Percepatan gravitasi di berbagai tempat di Bumi.

tempat	lintang (°)	ketinggian (m)	percepatan gravitasi (m/s2)
Kutub Utara	90	0	9,832
Greenland	70	20	9,825
Stockholm	59	45	9,818
Brussels	51	102	9,811
Banff	51	1.376	9,808
New York	41	38	9,803
Chicago	42	182	9,803
Denver	40	1.638	9,796
San Fransisco	38	114	9,800
Canal Zone	9	6	9,782

Newton Meets Kepler

Newton dapat menunjukkan bahwa Hukum Kepler dapat diturunkan secara matematis dari Hukum Gravitasi Universal dan Hukum Gerak Benda. Dalam penurunannya, digunakan kalkulus dan transformasi koordinat. (Silakan lihat Gara-Gara Gravitasi!) Rumit memang, tapi dapat dilakukan perhitungan sederhana untuk menggambarkan hubungan antara Hukum Newton dan Hukum III Kepler.

Akan dianalisis gerak melingkar planet. Asumsi gerak melingkar planet dapat digunakan karena memang kenyataannya orbit sebagian besar planet hampir lingkaran. Diandaikan sebuah planet dengan massa m_1 bergerak mengelilingi Matahari yang massanya M_{Mat} dengan kelajuan v_1. Jika jarak antara planet dan Matahari R_1, maka berlaku hubungan berikut.

F_{gravitasi}=F_{sentripetal} \\ \Rightarrow G\frac{m_1 M_{Mat}}{R_1^2}=m_1\frac{v_1^2}{R_1} \\ \Rightarrow G\frac{M_{Mat}}{R_1}=v_1^2\cdots\cdots\left(19\right)

Jika periode planet ini adalah T_1, maka v_1=2\pi R_1/T_1 dan berlaku hubungan berikut.

G\frac{M_{Mat}}{R_1}=\frac{4\pi^2 R_1^2}{T_1^2} \\\Rightarrow \frac{T_1^2}{R_1^3}=\frac{4\pi^2}{M_{Mat}G}\cdots\cdots\left(20\right)

Untuk planet lain, berlaku hubungan yang sama.

\\\frac{T_2^2}{R_2^3}=\frac{4\pi^2}{M_{Mat}G}\cdots\cdots\left(21\right)

Jadi, \tfrac{T_1^2}{R_1^3}=\tfrac{T_2^2}{R_2^3}, serupa dengan Hukum III Kepler.

Tinjau kasus berikut! Periode Bumi mengelilingi Matahari yaitu satu tahun dan jarak Bumi-Matahari yaitu 1,5.10¹¹ m. Jika diketahui periode revolusi planet Mars yaitu 1,87 tahun, dapat dihitung jarak rata-rata Mars-Matahari.

\frac{T_{Bumi}^2}{R_{Bumi-Mat}^3}=\frac{T_{Mars}^2}{R_{Mars-Mat}^3} \\ \Rightarrow R_{Mars-Mat}=\left(\frac{T_{Mars}^2}{T_{Bumi}^2}\right)^{1/3}R_{Bumi-Mat} \\ \Rightarrow R_{Mars-Mat}=2,28\cdot 10^{11}\text{ m}\cdots\cdots\left(22\right)

Bacaan

Foster, Bob (1999), Terpadu Fisika, Jakarta, Erlangga
Kamajaya (2004), Pintar Fisika, Jakarta, Ganesha
Kanginan, Marthen (1999), Seribu Pena Fisika, Jakarta, Erlangga
Malasan, Hakim L. (2002), Sistem Tata Surya, Bandung, ITB
R., Taufik Ramlan (2003), Ilmu Pengetahuan Bumi dan Antariksa, Bandung, FPMIPA-UPI
Ruwanto, Bambang (2004), Asas-asas Fisika, Yogyakarta, Yudhistira
S., Amsor (2003), Tata Surya, Bandung, FPMIPA-UPI